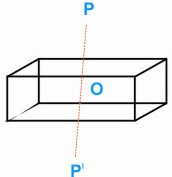
Consider a cuboid with a small cube cut out of a pair of
opposite corners. This modified block has no axis of rotational
symmetry or plane of symmetry, but it has symmetry about its
center O. For every point P on the block there is another
point P' such that O is the mid-point of PP'. This kind of
symmetry is called point symmetry.
A two-dimensional object
can only have point symmetry when it has rotational symmetry
about its center of even order.
Example of a Point Symmetry: