A reflection is a transformation which has the same effect
as a mirror. Every point P in front of a mirror (line or plane)
maps to an image point P' on the other side of the mirror
so that P’ and P are the same distance from the mirror,
and PP’ is at right angles to it.
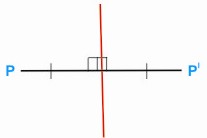
For example, a reflection
of the small English letter p in respect to a vertical line
would look like q. In order to reflect a planar figure one
needs the mirror to be a line (axis of reflection), while
for reflections in the three-dimensional space one would use
a plane for a mirror.
Reflection sometimes is considered as
a special case of inversion with infinite radius of the reference
circle. Geometrically, to find the reflection of a point one
drops a perpendicular from the point onto the line (plane)
used for reflection, and continues the same distance on the
other side.
To find the reflection
of a figure, one reflects each point in the figure. The effect on
any object is to produce an image of the same shape and size but
in the opposite sense. The matrix for reflection in a line through
the origin at an angle α to the x-axis is
Cos 2α Sin 2α
Sin 2α - Cos 2α