Two objects are similar when they have the sample shape but different
size. Paper is introduced in different sizes, A1, A2, A3,
A4 and A5, each one being half the size of the one before
it, but all the same shape. When a photograph is enlarged
to different sizes, all the objects in the photos change size
but not shape, so they are similar. Different commodities
such as soap powders and breakfast cereals are often sold
in cartoons of the same shape but different sizes.
Two shapes such
as the qudrilateral ABCD and PQRS are similar when the angles which
corresponds to one another are equal:
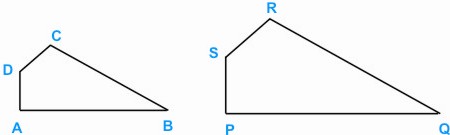
∠ A = ∠P; ∠B
= ∠Q, ∠C = ∠R, ∠D = ∠S and the ratios of the lengths of the corresponding
sides are also equal. In the example shown PQ:AB = QR:BC = RS:CD
= SP:DA = 2:1 where the linear scale factor is 2.
When two shapes
are similar, the ratio of their areas is equal to the square of
the ratio of their corresponding lengths, so the area of PQRS is
22 = 4 times the area of ABCD.
The enlargement transformation maps
any shape onto a similar shape.